高斯分布
高斯分布表达式
一元高斯分布
多元高斯分布
性质
高斯分布依赖于下面二次型,即马氏距离
协方差矩阵$\sum $可以取对称矩阵,任何非对称项都会从指数中消失(也可以从协方差矩阵定义看)可分解成对角矩阵
\begin{array}{l}{\Delta^{2}=[(\vec{X}-\vec{\mu})]^{\top}\left(Q \Lambda Q^{\top}\right)^{-1}[(\vec{X}-\vec{\mu})]} \\ {=\left[Q^{\top}(\vec{X}-\vec{\mu})\right]^{\top} \Lambda^{-1}\left[Q^{\top}(\vec{X}-\vec{\mu})\right]} \\ {=\left[Q^{\top}(\vec{X}-\vec{\mu})\right]^{\top}\left(\Lambda^{-\frac{1}{2}}\right)^{\top} \Lambda^{-\frac{1}{2}}\left[Q^{\top}(\vec{X}-\vec{\mu})\right]} \\ {=\left[\Lambda^{-\frac{1}{2}} Q^{\top}(\vec{X}-\vec{\mu})\right]^{\top}\left[\begin{array}{c}{\Lambda^{-\frac{1}{2}} Q^{\top}(\vec{X}-\vec{\mu})}\end{array}\right]} \\ {=\left[\left(Q \Lambda^{-\frac{1}{2}}\right)^{\top}(\vec{X}-\vec{\mu})\right]^{\top}\left[\left(Q \Lambda^{-\frac{1}{2}}\right)^{\top}(\vec{X}-\vec{\mu})\right]}\end{array}
含义:高斯分布中心在u,平移u之后高斯分布中心到原点,高斯分布椭圆轴拉伸变换成正圆,称一个旋转矩阵,将之前椭圆轴方向旋转到全局坐标系(Oxyz),特别注意:变换矩阵Q
椭圆中心u,轴方向:变换矩阵Q的列向量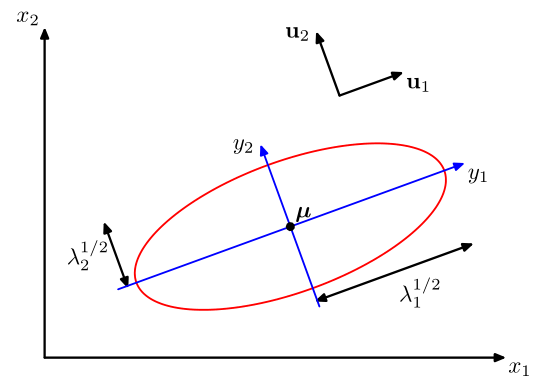
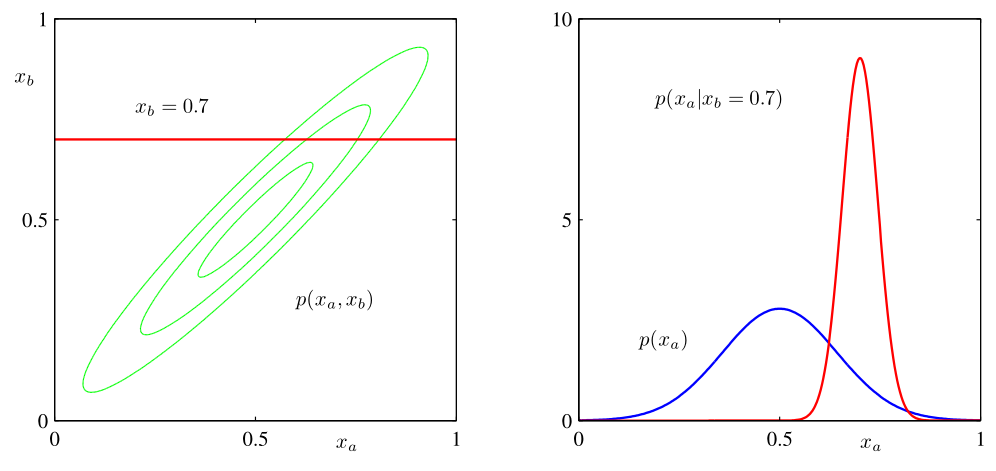
条件高斯分布
多元⾼斯分布的⼀个重要性质是,如果两组变量是联合⾼斯分布,那么以⼀组变量为条件,
另⼀组变量同样是⾼斯分布。类似地,任何⼀个变量的边缘分布也是⾼斯分布
协方差矩阵&精度矩阵&分块矩阵求逆
分块矩阵求逆
其中 $M=\left(A-B D^{-1} C\right)^{-}$
完全平方项
通过对比二次型找到均值何方差的表达式
分解式如下
二次型
条件概率均值和协方差
边缘高斯分布
分解式对变量Xb积分
关于Xb的项
其中 $\boldsymbol{m}=\boldsymbol{\Lambda}_{b b} \boldsymbol{\mu}_{b}-\boldsymbol{\Lambda}_{b a}\left(\boldsymbol{x}_{a}-\boldsymbol{\mu}_{a}\right)$
容易求得变量的积分 现在看剩余部分变量Xa和常量
通过对比得
总结
对联合高斯分布
条件概率
边缘概率
引用
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以邮件至 yangbenbo@whu.edu.cn
文章标题:高斯分布
本文作者:杨本泊
发布时间:2019-10-16, 13:30:27
最后更新:2023-07-09, 07:10:12
原始链接:http://yangbenbo.github.io/2019/10/16/高斯分布/版权声明: "署名-非商用-相同方式共享 4.0" 转载请保留原文链接及作者。