Github SSH Key避免Hexo部署输入密码

先来看广义逆阵

广义逆阵

广义逆也称为伪逆（pseudoinverse），有些时候，伪逆特指摩尔－彭若斯广义逆(M-P逆)。

种类

彭若斯条件

$$\begin{aligned} &A A^{\mathrm{g}} A=A\\ &A^{\mathrm{g}} A A^{\mathrm{g}}=A^{g}\\ &\left(A A^{\mathrm{g}}\right)^{\mathrm{T}}=A A^{\mathrm{g}}\\ &\left(A^{\mathrm{g}} A\right)^{\mathrm{T}}=A^{\mathrm{g}} A \end{aligned}$$

若${A^{\rm{g}}}$满足条件1,则为A的广义逆阵;满足条件1和2,则为A的广义反身逆阵;
4个条件都满足则为摩尔-彭若斯逆(M-P逆)

除此之外还有其他广义逆阵包括左侧逆阵,右侧逆阵等

应用

求解线性方程组

$$\eqalign{ & Ax = b \cr & x = {A^{\rm{g}}}b + \left[ {I - {A^{\rm{g}}}A} \right]w \cr}$$

M-P逆

任意矩阵都存在M-P逆,且唯一,是应用最广泛的一种逆矩阵

计算方法

1. 满秩分解

   $$\begin{aligned} \mathbf{A}=\mathbf{B C}, \mathbf{B} \in \mathbf{C}^{n \times r}, \mathbf{C} \in \mathbf{C}^{r \times n}, & \operatorname{rank}(\mathbf{B})=\operatorname{rank}(\mathbf{C})=r \\ \mathbf{A}^{+}=\mathbf{C}^{\mathrm{H}}\left(\mathbf{C} \mathbf{C}^{\mathrm{H}}\right)^{-1}\left(\mathbf{B}^{\mathrm{H}} \mathbf{B}\right)^{-1} \mathbf{B}^{\mathrm{H}} \end{aligned}$$

2. 奇异值分解svd

   $$\begin{aligned} &A=U\left(\begin{array}{ll} {\Delta} & {0} \\ {0} & {0} \end{array}\right) V^{H}\\ &A^{+}=V\left(\begin{array}{cc} {\Delta^{-1}} & {0} \\ {0} & {0} \end{array}\right)^{\mathrm{H}} U^{H} \end{aligned}$$

雅克比矩阵零空间

雅克比矩阵是关节空间到笛卡尔空间(机械臂末端)的映射,求解方程得

$$\matrix{ {\delta x = J\delta q} \hfill \cr {\delta q = {J^\# }\delta x + \left[ {I - {J^\# }J} \right]\delta {q_0}} \hfill \cr }$$

其中${J^\# }$为J的伪逆矩阵,从这里可以看出对于冗余机械臂(此时雅克比矩阵具有零空间)
可以在保证末端位置不变的情况下关节运动

冗余机械臂关节空间力矩

推导过程在pdf已经很详细了,这里摘取结论,资料出自Advanced Robotic Manipulation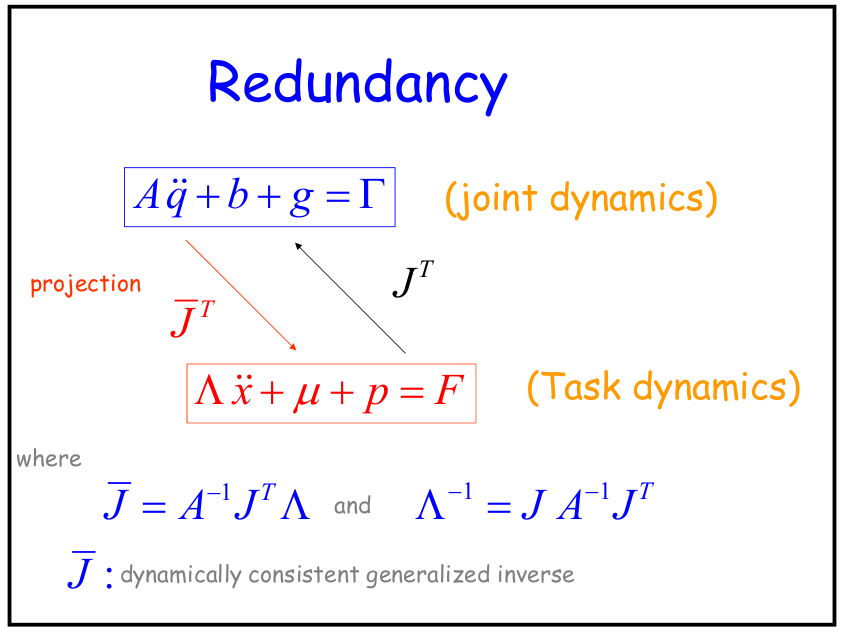

这里需要注意的是关节空间线性方程组求解时选择不同伪逆会有不同结果在pdf里面推导出来的逆是为了保证在对应零空间施加关节力矩不会影响操作空间加速度

不清楚的是franka笛卡尔空间阻抗控制
以及这里使用的矩阵求伪逆多了一个参数的作用

引用

1. 维基百科:广义逆阵
2. 雅克比矩阵零空间
3. ROBOT CONTROL PART 5: CONTROLLING IN THE NULL SPACE
4. 冗余机器人以及雅克比伪逆矩阵
5. 斯坦福课程:Advanced Robotic Manipulation
6. 书籍:矩阵论 杨明 刘先忠 华中科技大学出版社

---

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可以邮件至 yangbenbo@whu.edu.cn