Github SSH Key避免Hexo部署输入密码

这里取8位有符号数来说明

原码,反码,补码

这里针对有符号数

• 原码:最高位表示符号,整数为0,负数为1,其余部分为数绝对值的二进制表示.如-3 表示为1000 0011
• 反码:正数反码为本身,负数,保留符号位,其余位取反
• 补码:整数补码为本身,负数,保留符号位,其余为取反加1
• 形式值:将符号位作为实际含义,1000 0001 原码表示-1 ,形式值表示2^7+2^0 (考虑符号位)

计算机的加减乘除是最基本的运算,需要设计得尽可能简单,设计的初衷就是想用一种编码实现加减 a-b = a+(-b)

1. 原码,人脑最容易理解的方式,但是计算机不同,需要额外处理符号位是很麻烦,
   1-1=0000 0001(原)+1000 0001(原)=1000 0010(原)=-2 这是不符号运算的

2. 反码,原码1000 0110 的补码是1111 1001.可以看出负数的补码(形式值)与自身的绝对值之和为1111 1111 (255)
   这里只看数值运算,结合整数的补码就是本身,反码的实质就是取余运算 %1111 1111 (mod 255),理解可结合下面这张图
   
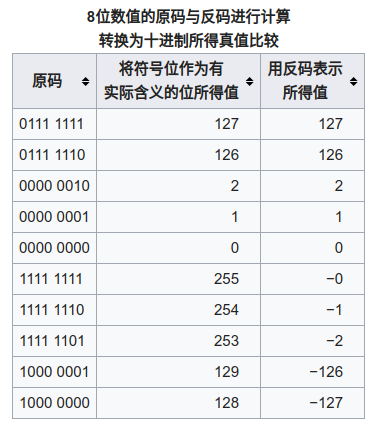
   还有一种理解:不看符号位,对于数值部分取反之后和之前和恒为0111 1111,可以看出是对数值部分取余即%0111 1111(%127).

   反码存在的问题,

   1. 0 的表示有两种,浪费了一个二进制数 0000 0000(原) 1000 0000(原) 反码分别是0000 0000 和 1111 1111
   2. 无法保证减法运算,如 2-1 = 0000 0010(反) + 1111 1110(反) = 0000 0000(原)
      1-1 之类是对的1111 1111(反) = 1000 0000(原)

3. 补码,同反码一样,不过多了+1,相当于%256 (1000 0000)

   1. 引入加1之后巧妙解决了0的表示问题,0000 0000(原) 和1000 0000(原)对应的补码都是0000 0000(补)
      那现在用1000 0000表示什么数呢? 1000 0000(补) + 0000 0001(补)=1000 0001(补)=1111 1111(原)=-127
      所以用1000 0000表示-128,没有对应的原码和反码 所以8为有符号二进制为[-128,127]

   2. 保证了减法运算,这里用了同余的性质

      $$\left.\begin{array}{l} a \equiv b(\bmod m) \\ c \equiv d(\bmod m) \end{array}\right\} \Rightarrow\left\{\begin{array}{c} a \pm c \equiv b \pm d(\bmod m) \\ a c \equiv b d(\bmod m) \end{array}\right.$$

      如(2-1)%256 = (2 + (-1))%256 = (2+(-1%256)) %256 = 1 最后一步%256 是通过高位溢出达到的

   3. 用补码的第二种解释%128,解释为什么负数补码的补码就是负数本身,因为保留了符号位,数值部分两次取余%128%128为本身
      如给定1000 0001(原),则取补码为1111 1111(补),再求补码1000 0001

   4. 但是为什么反码不对呢?反码也是取余,主要是因为反码0的两种表示方式值相差1

      0+1 = 1000 0000(原) + 0000 0001(原)=1111 1111(反)+0000 0001(反)=0000 0000=0
      即0+1=0;这才是问题所在,0的两种表达方式导致了溢出处理有问题

补码性质

写这里是因为一道剑指offer的题解,很精妙:输入一个整数,输出该数二进制表示中1的个数.其中负数用补码表示.

首先需要说明的是数在计算机中存储是用补码的形式

针对a-1的问题

1. 首先看正数,a-1 就是a的二进制从右至左第一位1借位,对应位变0,右边的都变成1 如0000 1100 - 1 = 0000 1011
2. 负数,还是要用到同余 (a-1)%256 = ((a%256)-1)%256 如(-5-1)%256 等式左边=250=右边=1111 1010-1=1111 1001 同正数一样
   总的来说补码表示的数可以直接按照正数的加减法来运算(包括-1),这也是补码设计的初衷:统一加减法即计算机运算直接用补码的形式值来计算,输出转换为原码就可以了

注意:负数右移或者/2左边补1,最小的数是-1(即1111 1111),所以在求一个数有多少位1时不要动这个数,而是移动取的位,比如a & b,是把b左移,而不是把原数右移

引用

1. 原码、反码、补码知识详细讲解（此作者是我找到的讲的最细最明白的一个）
2. 维基百科:补码
3. 同余

---

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可以邮件至 yangbenbo@whu.edu.cn