根轨迹
根轨迹定义
一个基本的反馈系统传递函数为
极点为分母等于0时对应的根,换一种方式,求解根在K从0到无穷大对应的轨迹,
就可以得到不同K下系统的极点,从而得到系统的脉冲响应函数
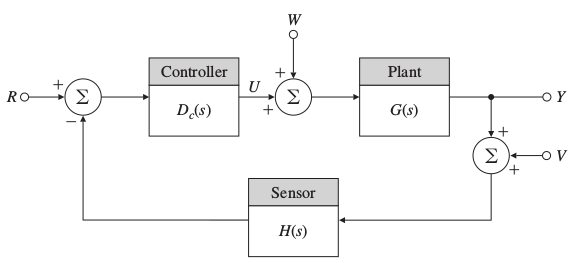
根轨迹不局限于系统增益K,也可以求解相对于任何在特征方程中线性的参数的根轨迹
比如在求解K=1是不同c下的根轨迹
根轨迹准则
L(s)
- b(s) 极点个数为n 用x表示
- a(s) 零点个数为m 用o表示
n条根轨迹从L(s)极点出发,m条轨迹终止于L(s)零点;
n>m,则有n-m条根轨迹从极点指向无穷,反之m-n条轨迹从无穷指向零点从根轨迹公式 $a(s)+K b(s)=0$ 可以得出K=0时,a(s)=0,即为L(s)的极点,K趋向于无穷时,b(s)=0,为L(s)的零点
根轨迹在实轴上从左往右奇数点左边有根轨迹.
根轨迹方程的一种表示 $L(s)=-\frac{1}{K}$ 从复数相位看左边的相位=右边的相位=180°
- 用$\psi_{i}$表示零点对应项在复平面上任意一点对应的相角度,即零点指向对应点构成向量的角度
用$\phi_{i}$表示极点对应项在复平面上任意一点对应的相角度,即极点点指向对应点构成向量的角度
为保证相位不难理解实轴上根轨迹需要在奇数点左边
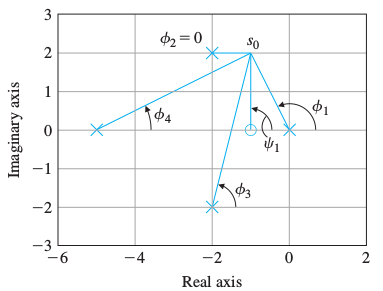
对于很大的s和K,n-m条根轨迹的渐近线为从实轴上中心点 $s=\alpha$出发的射线,射线角度 $\phi_{l}$
当K很大时变换根轨迹方程
从而得到
一或多个极点从一个点离开的方向
可以用一个很靠近极点的点来推导角度,到达零点的方向也可类似推导
可用于靠近虚轴方向的判断,看是否忘复平面左边走
同一个点可以有q个根,从点离开的方向
应用
- 超前补偿器:|z|<|p|
- 滞后补偿器:|p|<|z|
可以看补偿器的伯德图来理解
引用
- Feedback Control of Dynamic Systems by Gene F. Franklin
- DR_CAN自动控制原理
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以邮件至 yangbenbo@whu.edu.cn
文章标题:根轨迹
本文作者:杨本泊
发布时间:2020-03-28, 17:02:54
最后更新:2023-07-09, 07:10:12
原始链接:http://yangbenbo.github.io/2020/03/28/根轨迹/版权声明: "署名-非商用-相同方式共享 4.0" 转载请保留原文链接及作者。