逆运动学
逆运动学
逆运动学是已知机械臂末端的位姿求解关节角度的过程,通常有两种方法:
- 解析法.使用代数或者几何法求解,可以求得当前位姿对应的所有解,需要选择离当前位置最近的关节角解缺点是机械臂需要满足一定的要求.
- 优化法.把问题转化为优化问题(很多问题都可以转化为优化问题),缺点是只能获得一个解,耗时相对较长
解析法
虽然优化法有很多优势,但是逆解通常多解,使用解析法可以得到所有解,方便对优化解进行理解.这里针对普通的6自由度机械臂进行分析,通常有8组解,分别由位置和姿态贡献.下图是puma机械臂前3个自由度构型,后3个自由度对应ZYX欧拉角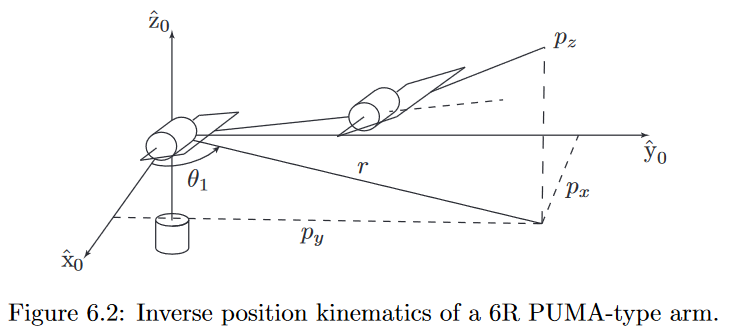
- 位置逆解
如下图所示,主要有4种构型对应4个解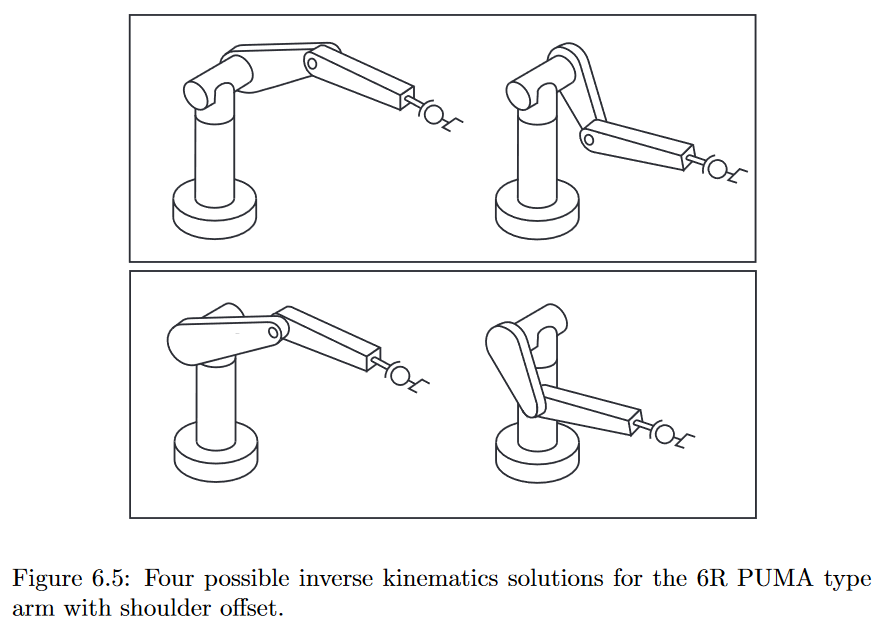
- 姿态逆解
欧拉角1可以表示姿态,也可以反过来更好理解理论逆解.比如根据最后3个关节定义坐标系,ZYX欧拉角可以表示分别转动R4R5R6之后工具的新姿态,那么可以反过来给定姿态之后通过求欧拉角得到具体的关节角度.这里不只是ZYX欧拉角,通过定义关节角度在不同的零位也可以得到如ZYZ欧拉角等等.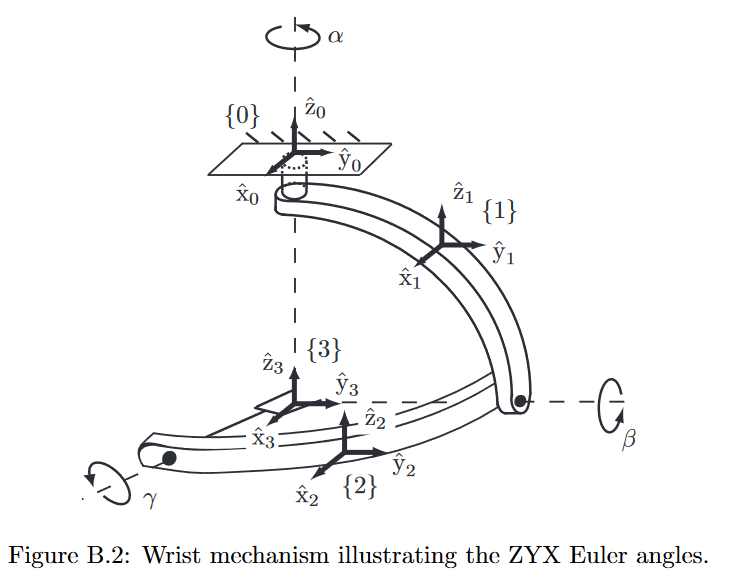
欧拉角ZYX既可以看成是相对动坐标系依次绕着Z,Y,X转动,也可以看成是相对基坐标系依次绕着X,Y,Z轴转动这里附带说明RPY(roll偏航,pitch俯仰,yaw滚动),通常针对船只航行或者飞机飞行.通常定义向前为x(机械臂夹爪也是),所以通常Roll Axis是x轴,即ZYX欧拉角对应yaw, pitch and roll. 而RPY可以看成绕着固定坐标系分别进行xyz轴旋转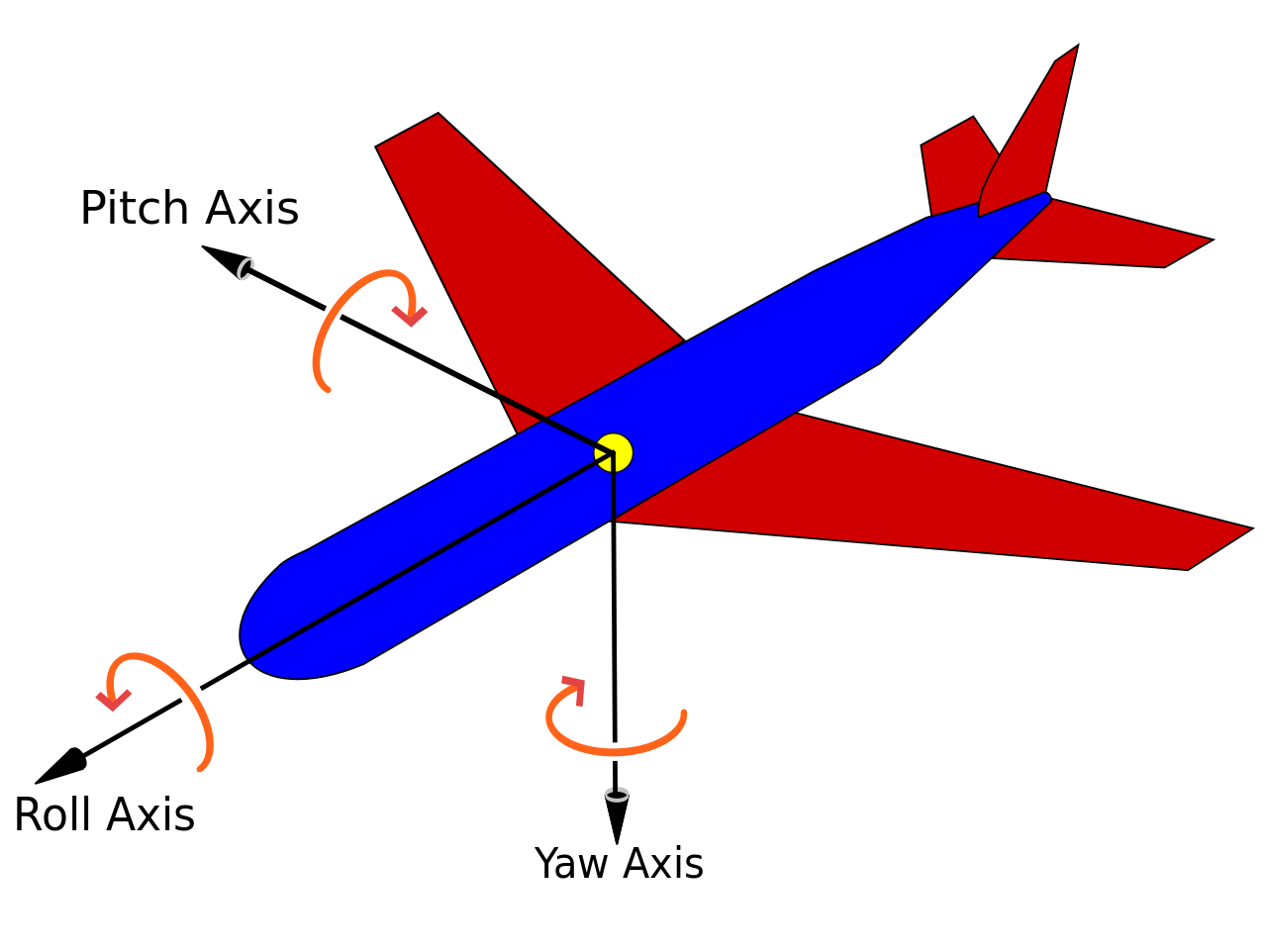
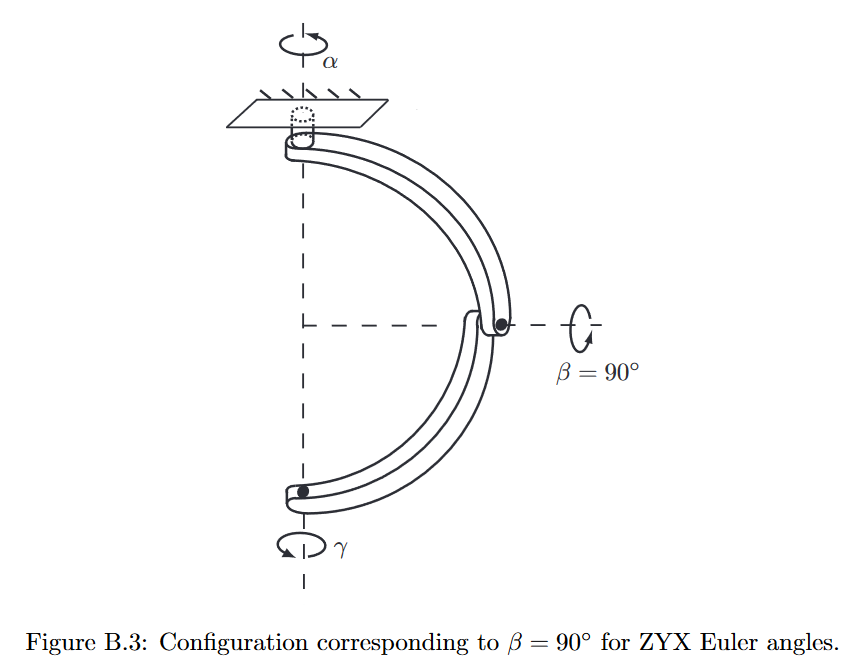
对ZYX欧拉角展开后得到针对RPY角度满足$\alpha,\beta,\gamma \in (-\pi,\pi]$,则存在2种情况 - 只有1个解, $c_{\beta}=0$, 即$r_{31}=1$, 对应$\beta =-\frac{\pi}{2}$;$r_{31}=-1$, 对应$\beta =\frac{\pi}{2}$.这两种情况对应奇异,即第1个和第3个轴重合,有无穷多组解
- 存在2个解. 可以分成两步理解,分成轴线朝向2自由度+绕轴线转动自由度.轴线朝向自由度又可看成球面,通过第一个轴再旋转180°,俯仰角反向对称对应另外一个解
- $c_{\beta}>0$,
- $c_{\beta}<0$
优化法
雅克比逆(牛顿-拉夫森法, Newton-Raphson Method)
逆运动学就是求解方程$f(\theta)=0$,目标是找到关节坐标满足$x_{d}-f\left(\theta_{d}\right)=0$,使用泰勒展开,即只保留泰勒级数到第一项,简化为
如果作则雅克比矩阵可逆,则有
如果正向运行学$f(\theta)$是$\theta$的线性函数,泰勒级数没有高阶项,新的估计值$\theta_{1}=\theta_{0}+\Delta \theta$精确满足运动学方程,
相反,如果运动学是非线性函数,那么新的估计值将会更接近真实值,迭代不断重复,直到$\theta$收敛,如下图所示
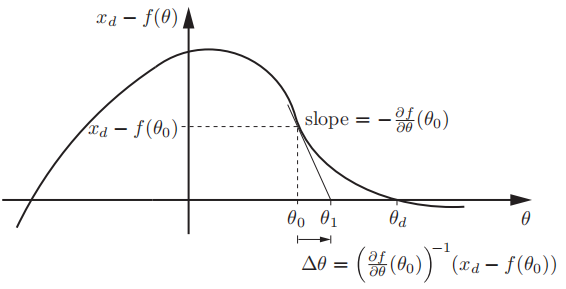
如果逆运动学存在多组解,则只会找到最近的解.在实际使用中,矩阵求逆很耗费计算资源,通常是借鉴$A x=b$,使用矩阵的LU分解.如果雅克比不可逆,则使用矩阵伪逆(Moore-Penrose),伪逆求法:
- SVD分解, 然后求逆
- 行满秩,右逆 $J^{\dagger}=J^{T}\left(J J^{T}\right)^{-1}$
列满秩,左逆 $J^{\dagger}=\left(J^{T} J\right)^{-1} J^{T}$
使用伪逆得到的解不会精确满足方程,但从最小二乘的层面会尽可能接近这个条件,求线性方程组或者拟合的时候经常用到.伪逆推导就是求解然后使用拉格朗日乘数法(Lagrange Multiplier)2 变成
分别对两个变量求导等与0得到两个方程求解就得到了右伪逆.
顺带说一下雅克比的零空间(null space),把关节速度投影到”零空间内”,对末端运动没有影响,公式如下,可以参考我的另一篇文章雅克比矩阵零空间上述方法只是针对机械臂的末端位置求解,如果增加姿态,则不能只是直接简单相减,使用雅克比我们可以先求出末端的线速度和角速度(物体的速度旋量)
首先计算相对物体坐标系的期望位形
其中b指代body,即当前末端位恣,d指代destination.然后使用矩阵对数求解旋量
然后迭代求解
注意这里使用的是物体雅克比(Body Jacobian)和对应的物体运动旋量(Body Twist),如果使用空间雅克比和空间运动旋量需要转换一下,$\mathcal{V}_{s}=\left[\mathrm{Ad}_{T_{s b}}\right] \mathcal{V}_{b}$
雅克比逆的方法也可以理解从当前点到目标点的速度,然后用雅克比逆求解关节角速度,使用到下一个关节角度的叠加,
只是这种理解关节角度角度变化不能太大,否则雅克比不准(和关节构型有关,是变化的)
雅克比转置(梯度下降法)
逆解的目标是当前的位置距离目标位置尽可能近,转化为一个最小值问题这里有系数只是为了求导后没有系数,不影响结果,将当前位置带入方程得
这个时候可以使用梯度下降法,每一步都沿着下降最快的方向走,方向为梯度的反方向
其中$\alpha$是梯度下降法的一个系数,步长(step size)或这学习效率(learning rate).步长太大导致”走过头”甚至多绕弯路,
最终迭代速度慢(甚至无法收敛),步长太小导致迭代速度太慢.雅克比转置方法不需要求逆,不过收敛速度反而慢一点,使用这个方法控制机械臂,离end effector较远的关节常常需要输出更大的扭矩。
阻尼最小二平方法(DLS, Damped Least Square), 也叫Levenberg-Marquardt method
雅克比奇异导致关节速度过大,这显然是我们不希望看到的,现在也有很多避奇异的方法,DLS就是一种限制关节速度的方法,
这时我们需要最小化的目标是即把关节变化量放进最小化的目标函数,方程可等价于
借鉴线性方程组$A x=b$求解(伪逆)
进而得到
由于左侧矩阵非奇异,则有
同时有$\left(J^{T} J+\lambda^{2} I\right)^{-1} J^{T}=J^{T}\left(J J^{T}+\lambda^{2} I\right)^{-1}$ 可以左右两侧同时乘$J^{T} J+\lambda^{2} I$
则有这就是DLS方法的迭代方程
在编程实现中,通常是直接处理雅克比矩阵奇异值分解后对奇异值操作,这是等效的,首先奇异值分解
然后化简得到
从这里可以看出E为对称矩阵,而且值为(雅克比矩阵svd分解后奇异值为$\sigma_i$,求逆之后为倒数)
所以一种比较简单的方式就是直接处理奇异值,kuka-lwr就是这样处理的
总结: DLS方法可以看成是两种方法的结合,
当$\lambda$很小时,根据SVD分解奇异值可以看出来就是牛顿-拉夫森法(矩阵逆),
当$\lambda$很大, $J{J^T}$为对阵矩阵,可以分解为,由于分解后的特征值相对$\lambda$ 很小,则最后直接成为下式,其实就是前面的梯度法
逆解参考Samuel R. Buss的Introduction to Inverse Kinematics with Jacobian Transpose, Pseudoinverse and Damped Least Squares methods
拉格朗日乘子法
一种寻找多元函数在其变量受到一个或多个条件的约束时的局部极值的方法。这种方法可以将一个有$n$个变量与$k$个约束条件的最优化问题转换为一个解有$n + k$个变量的方程组的解的问题
拉格朗日函数如下,
其中$f(x)$为目标函数$g(x)=0$为约束条件. 为找到拉格朗日函数极值,即偏微分=0,对应$\frac{\partial \mathcal{L}}{\partial x}=0,\frac{\partial \mathcal{L}}{\partial \lambda}=0 $
等价为
既包含了原本的约束,同时在约束条件下满足$\frac{\partial f(x)}{\partial x}=0$, 对应找到极值.
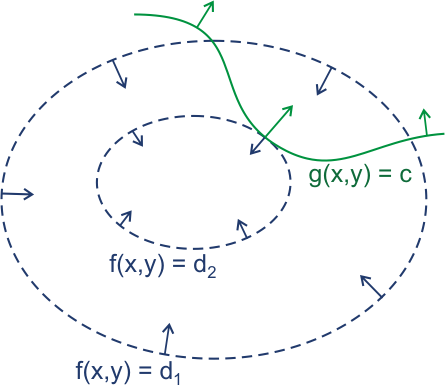
直观理解2自变量单约束条件如下, 极值点对应目标函数与约束函数的梯度方向共线$\nabla f\left(x,y\right)=- \lambda \nabla g\left(x,y\right)$, 对应$\nabla (f\left(x,y\right)+\lambda g\left(x,y\right))=0$, 即沿着约束曲面(曲线走)没有分量能够让目标函数变化.如下图所示
matlab
Robotics System Toolbox 中逆解模块Inverse Kinematics Algorithms3主要使用2种算法
- BFGS Gradient Projection:
- Levenberg-Marquardt:
遇到的问题
使用trac-ik求解motoman逆运动学的时候容易求到距离当前关节较远的位置
通过判断关节角度差来决定是否需要重新逆解即可
引用
- 干货 | “逆运动学”——从操作空间到关节空间(上篇)
- 干货 | “逆运动学”——从操作空间到关节空间(下篇)
- MODERN ROBOTICS MECHANICS, PLANNING, AND CONTROL
1. https://en.wikipedia.org/wiki/Euler_angles ↩
2. https://en.wikipedia.org/wiki/Lagrange_multiplier ↩
3. https://ww2.mathworks.cn/help/robotics/ug/inverse-kinematics-algorithms.html#bve7apt ↩
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以邮件至 yangbenbo@whu.edu.cn
文章标题:逆运动学
本文作者:杨本泊
发布时间:2020-11-23, 13:37:45
最后更新:2024-06-23, 21:53:48
原始链接:http://yangbenbo.github.io/2020/11/23/逆运动学/版权声明: "署名-非商用-相同方式共享 4.0" 转载请保留原文链接及作者。