Github SSH Key避免Hexo部署输入密码

• 机械臂动力学
  • 牛顿欧拉递推动力学

机械臂动力学

动力学主要研究:

• 已知轨迹点求期望的关机力矩,用于机械臂控制
• 已知力矩求机械臂运动的轨迹点,用于仿真

牛顿欧拉递推动力学

牛顿欧拉递推动力学是一种高效的动力学计算方法

基础知识

• ${ }^{B} V_{Q}$: $Q$点在坐标系$\{B\}$中求导并表示
• ${ }^A({ }^{B} V_{Q})$: $Q$点在坐标系$\{B\}$中求导并在坐标系$\{A\}$中表示
• $v_c = { }^{U} V_{CORG}$: 坐标系$\{C\}$原点在常见坐标系$\{U\}$中求导并表示
• ${ }^{A} v_c = { }^B_A R { }^{U} V_{CORG}$: 坐标系$\{C\}$原点在常见坐标系$\{U\}$中求导并表示
• ${ }^{A} \Omega_{B}$: 坐标系$\{B\}$相对于坐标系$\{A\}$的旋转角速度
• $w_c = { }^{U} \Omega_{C}$: 坐标系$\{C\}$相对于世界坐标系$\{U\}$的旋转角速度
• ${}^Aw_c = {}^A_UR{ }^{U} \Omega_{C}$: 坐标系$\{C\}$相对于世界坐标系$\{U\}$的旋转角速度在坐标系$\{A\}$中的表示

刚体线速度/线加速度

坐标系$\{A\}$固定,$\{B\}$与$\{A\}$的原点重合,则$\{B\}$中一点$Q$的速度为:

$${ }^{A} V_{Q}={ }_{B}^{A} R^{B} V_{Q}+{ }^{A} \Omega_{B} \times{ }_{B}^{A} R^{B} Q$$

扩展到原点不重合:

$${ }^{A} V_{Q}={}^AV_Q + { }_{B}^{A} R^{B} V_{Q}+{ }^{A} \Omega_{B} \times{ }_{B}^{A} R^{B} Q$$

求导得:

$$\begin{aligned} { }^{A} V_{Q}={ }^{A} \dot{V}_{B O R G} &+{ }_{B}^{A} R^{B} \dot{V}_{Q}+2^{A} \Omega_{B} \times{ }_{B}^{A} R^{B} V_{Q}+{ }^{A} \dot{\Omega}_{B} \times{ }_{B}^{A} R^{B} Q \\ &+{ }^{A} \Omega_{B} \times\left({ }^{A} \Omega_{B} \times{ }_{B}^{A} R^{B} Q\right) \end{aligned}$$

此式子可根据不同情况进行简化,比如${}^BQ$是常量时${ }^{B} V_{Q}={ }^{B} \dot{V}_{Q}=0$

角速度/角加速度

$\{B\}$相对于于$\{A\}$的角速度${}^A\Omega_B$,$\{C\}$相对于于$\{B\}$的角速度${}^B\Omega_C$,则有

$${ }^{A} \Omega_{C}={ }^{A} \Omega_{B}+{ }_{B}^{A} R^{B} \Omega_{C}$$

求导得:

$${ }^{A} \dot{\Omega}_{C}={ }^{A} \dot{\Omega}_{B}+{ }_{B}^{A} R^{B} \dot{\Omega}_{C}+{ }^{A} \Omega_{B} \times{ }_{B}^{A} R^{B} \Omega_{C}$$

连杆速度传递

机械臂关节坐标系如图所示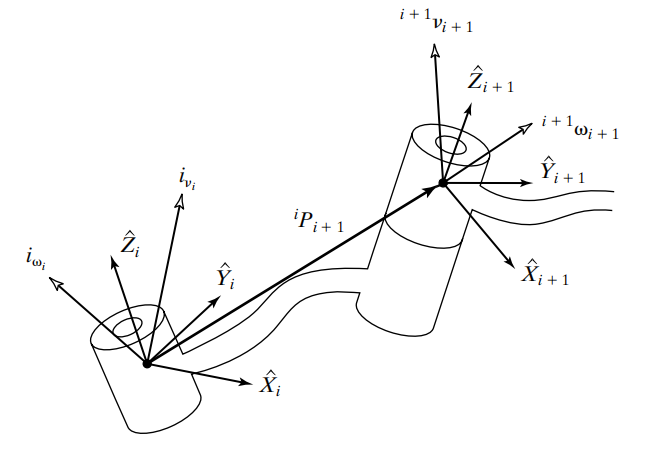

1. 直接采用前面推论进行替换得到最终的表达式
   角速度/角加速度推导

   • 坐标系$\{A\}$替换为坐标系$\{0\}$(世界坐标系),$\{B\}$替换为$\{i\}$,$\{Q\}$替换为$\{i+1\}$(可在$Q$点建立一个坐标系)

   • 替换完之后左乘矩阵${}^{i+1}_0R$即可得到最终表达时

     线速度/线加速度推导

   • 坐标系$\{A\}$替换为坐标系$\{0\}$(世界坐标系),$\{B\}$替换为$\{i\}$,$\{C\}$替换为$\{i+1\}$

   • 替换完之后左乘矩阵${}^{i+1}_0R$即可得到最终表达时

2. 直接求导推导
   世界坐标系下角速度:连杆的角速度等于上一个连杆的角速度加上由于关节转动带来的角速度

   $$\boldsymbol{\omega}_{i+1}=\boldsymbol{\omega}_{i}+\dot{\boldsymbol{\theta}}_{i+1} \boldsymbol{z}_{i+1}$$

   求导然后左乘${}^{i+1}_0R$即可得到角加速度表达式,借助公式${}^0_i \dot{\boldsymbol{R}} = {}^0 \omega_{i} \times {}^0_i\boldsymbol{R}$

   $${ }^{i+1} \dot{\omega}_{i+1}={ }_{i}^{i+1} R^{i} \dot{\omega}_{i}+{ }_{i}^{i+1} R^{i} \omega_{i} \times \dot{\theta}_{i+1}{ }^{i+1} \hat{z}_{i+1}+\ddot{\theta}_{i+1}{ }^{i+1} \hat{z}_{i+1}$$

   同理世界坐标系下线速度:连杆的线速度等于上一个连杆的线速度,上一个连杆转动带来的线速度,以及关节平移(移动关节才有)带来的速度之和

   $$\boldsymbol{v}_{i+1}=\boldsymbol{v}_{i}+\boldsymbol{\omega}_{i} \times ({}^0_iR{}^i\boldsymbol{p}_{i+1})+\dot{\boldsymbol{d}}_{i+1} \boldsymbol{z}_{i+1}$$

   ${}^0_iR{}^i\boldsymbol{p}_{i+1}$表示连杆坐标系$\{i\}$原点到$\{i+1\}$原点向量在世界坐标系下的表示
   求导即可得到线加速度关系,注意如果是移动关节,那么$\boldsymbol{p}_{i+1}$也是变化的所以才会有公式里面的倍数2,对应科式加速度

   $$\begin{aligned} { }^{i+1} \dot{v}_{i+1} &={ }_{i}^{i+1} R\left({ }^{i} \dot{\omega}_{i} \times{ }^{i} P_{i+1}+{ }^{i} \omega_{i} \times\left({ }^{i} \omega_{i} \times{ }^{i} P_{i+1}\right)+{ }^{i} \dot{v}_{i}\right) \\ &+2^{i+1} \omega_{i+1} \times \dot{d}_{i+1}{ }^{i+1} \hat{z}_{i+1}+\ddot{d}_{i+1}{ }^{i+1} \hat{z}_{i+1} \end{aligned}$$

   也可以根据绝对加速度=相对加速度+牵连加速度+科式加速度来计算,在之前的文章科式加速度中有提到过
   质心的加速度更明显一点

   $${}^i \dot{v}_{C_{i}}={}^i\dot{\omega}_{i} \times^{i} P_{C_{i}}+{ }^{i} \omega_{i} \times\left({ }^{i} \omega_{i} \times { }^{i} P_{C_{i}}\right)+^{i} \dot{v}_{i}$$

连杆力/力矩传递

不考虑重力,利用平衡方程递推关节力矩

$$\begin{array}{l} F_{i}=m \dot{v}_{c_{i}} \\ N_{i}=^{c_{i}} I \dot{\omega}_{i}+\omega_{i} \times^{c_{i}} I \omega_{i} \end{array}$$

得到转动关节递推算法:
外推:1->5:
${}^{i+1} \omega_{i+1}={ }_{i}^{i+1} R^{i} \omega_{i}+\dot{\theta}_{i+1}^{i+1} \hat{Z}_{i+1}$
${ }^{i+1} \dot{\omega}_{i+1} ={ }_{i}^{i+1} R^{i} \dot{\omega}_{i}+{ }_{i}^{i+1} R^{i} \omega_{i} \times \dot{\theta}_{i+1}^{i+1} \hat{Z}_{i+1}+\ddot{\theta}_{i+1}^{i+1} \hat{Z}_{i+1}$
${ }^{i+1} \dot{v}_{i+1} ={ }_{i}^{i+1} R\left({ }^{i} \dot{\omega}_{i} \times{ }^{i} P_{i+1}+{ }^{i} \omega_{i} \times\left({ }^{i} \omega_{i} \times{ }^{i} P_{i+1}\right)+{ }^{i} \dot{v}_{i}\right)$
${ }^{i+1} \dot{v}_{C_{i+1}} ={ }^{i+1} \dot{\omega}_{i+1} \times{ }^{i+1} P_{C_{i+1}}+{ }^{i+1} \omega_{i+1} \times\left({ }^{i+1} \omega_{i+1} \times{ }^{i+1} P_{C_{i+1}}\right)+{ }^{i+1} \dot{v}_{i+1} $
${ }^{i+1} F_{i+1} =m_{i+1}{ }^{i+1} \dot{v}_{C_{i+1}}$
${ }^{i+1} N_{i+1} ={}^{C_{i+1}} I_{i+1}{ }^{i+1} \dot{\omega}_{i+1}+{ }^{i+1} \omega_{i+1} \times {}^{C_{i+1}} I_{i+1}{ }^{i+1} \omega_{i+1}$

内推:6->1
${}^i f_{i}={ }_{i+1}^{i} R^{i+1} f_{i+1}+{ }^{i} F_{i}$
${ }^{i} n_{i}={ }^{i} N_{i}+{ }_{i+1}^{i} R^{i+1} n_{i+1}+{ }^{i} P_{C_{i}} \times{ }^{i} F_{i}+{ }^{i} P_{i+1} \times{ }_{i+1}^{i} R^{i+1} f_{i+1}$
$\tau_{i}={ }^{i} n_{i}^{T} i \hat{Z}_{i}$

考虑重力:令${ }^{0} \dot{v}_{0}=G$,其中$G$与重力大小相等,方向相反,等价于机器人以1g的加速度向上做加速运动

引用

1. 机器人学导论(Introduction to Robotics:Mechanics and Control)
2. 干货 | 机械臂的动力学（一）：牛顿欧拉法

---

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可以邮件至 yangbenbo@whu.edu.cn